Electrical conductivity measurement with eddy current - 6 factors you should pay attention to

What is electrical conductivity?

The following article describes these influential factors, their impact on measurement quality and the ways to minimize them.

1. Thermal effects in measurement

The electrical conductivity is a temperature-dependent variable. If the temperature changes, the temperature coefficient of the material plays an important role. For metals, the higher the temperature, the lower the conductivity. For example, the conductivity of copper drops from 58.0 MS/m at 20 °C to 56.9 MS/m at 25 °C. This is approximately 0.4 % per degree Celsius.

Conductivity is usually specified in relation to 20 °C. As soon as the test object has a temperature that deviates from 20 °C, the measured conductivity can be converted to the conductivity value at 20 °C according to the following equation (DIN 50994):

σ(20°C) = σ(T)⋅[1+α⋅(T-20°C)]

Typical temperature coefficients can be seen in Figure 1. However, some metals, such as titanium, deviate from the general trend. The values shown below were determined by the Physikalisch-Technische Bundesanstalt (PTB) in Braunschweig for 20 samples.

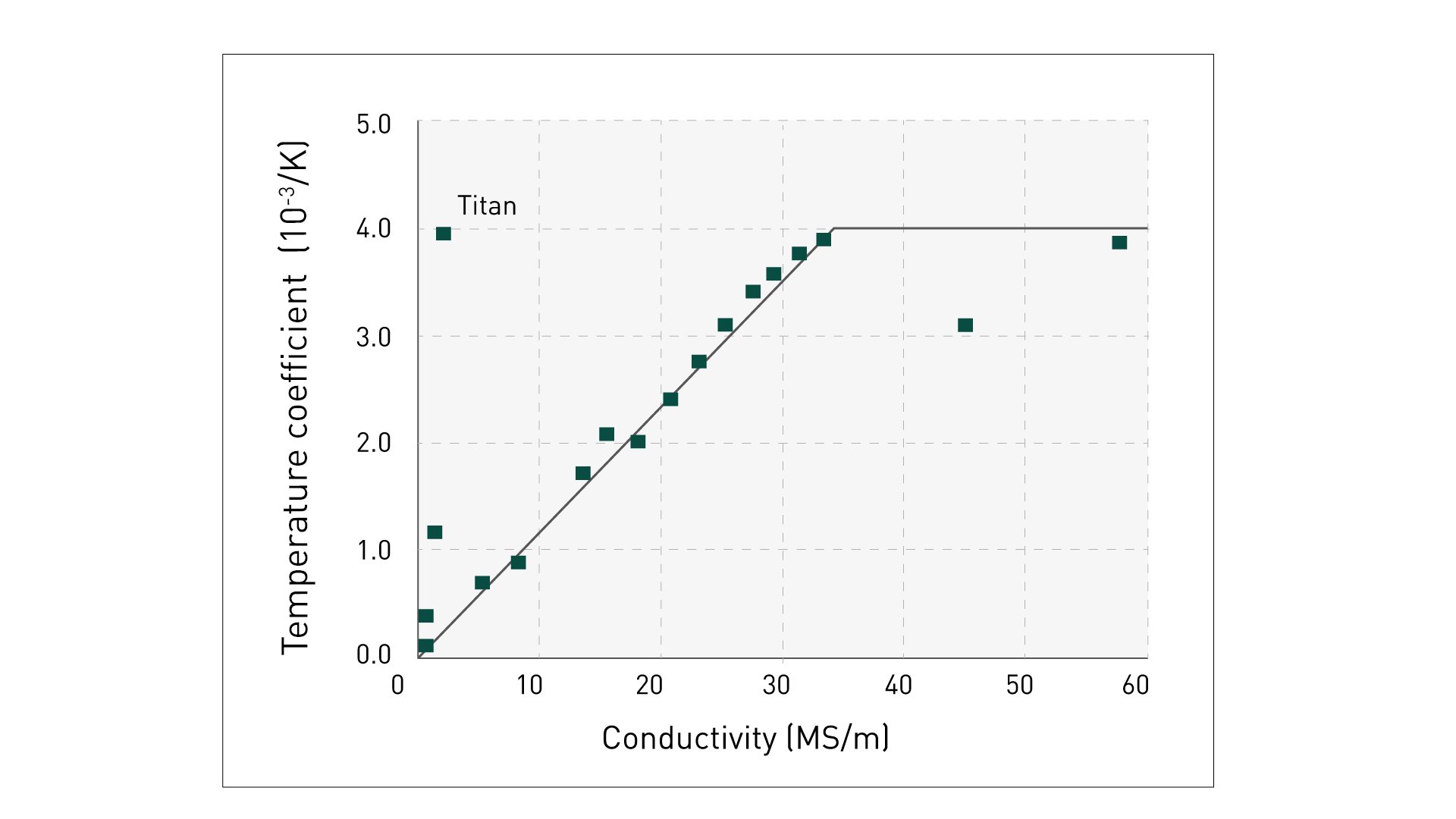Fig. 1: Typical temperature coefficients

The compensation of temperature can be performed directly or indirectly. In a direct temperature compensation, the temperature of the test object will be measured and the formula given above with the respective temperature coefficient will be applied. The temperature can be compensated indirectly by bringing the conductivity standards to the temperature of the test object for a two-point calibration. This raises the calibration curve of the measuring system to the new temperature range. Temperature-compensated measurements can then be performed.

2. Lift-off effects of the probe

A change in the distance of the eddy current probe to the measuring surface has a great influence on the measuring accuracy. Therefore, the eddy current measuring instruments on the market usually have the function of detecting the distance from the probe to the test object and compensating for this disturbing effect. In this way, measurement on thin coatings and foils is also possible.

Figure 2 shows the influence of the distance between the test object and the probe on the relative measurement error at 60 kHz, using four different types of conductivity as examples.

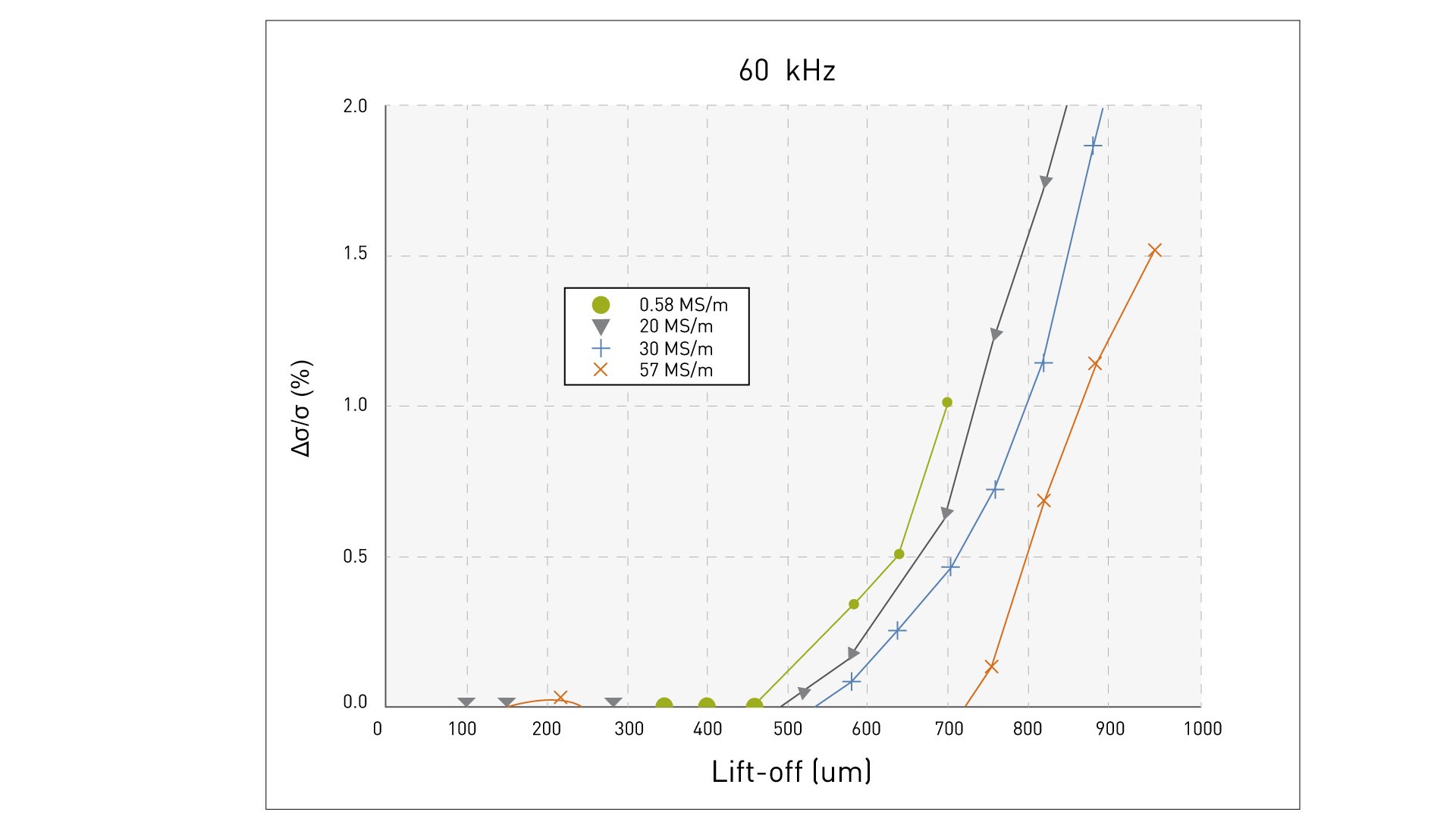
Fig. 2: Lift-off effects at 60 kHz

3. Material thickness of the test object

If the measured object is too thin, the magnetic field generated does not penetrate the material completely. That is to say, the eddy current density in the material is not only influenced by the conductivity, but additionally by the material thickness.

For this reason, it is essential to observe the critical minimum thickness of the measured object (see DIN 50994):

d_sat = 3 ⋅ δ₀

Where d₀ denotes the standard penetration depth at which the current density has decayed to 1/e:

δ_{0 = K ⋅ (503⋅10³)/√(f⋅σ)} 

This equation shows that high frequencies f lead to a low penetration depth (the so called "skin effect"). The measuring frequency can thus be set in order for the material thickness to be greater than the saturation thickness d_sat. Likewise, the penetration depth decreases with the growing conductivity of the material. K denotes the probe type-specific correction factor, which takes into account the inhomogeneity of the coil field as well as the inhomogeneity of the test object's material. In a first approximation, K = 1 can be set.

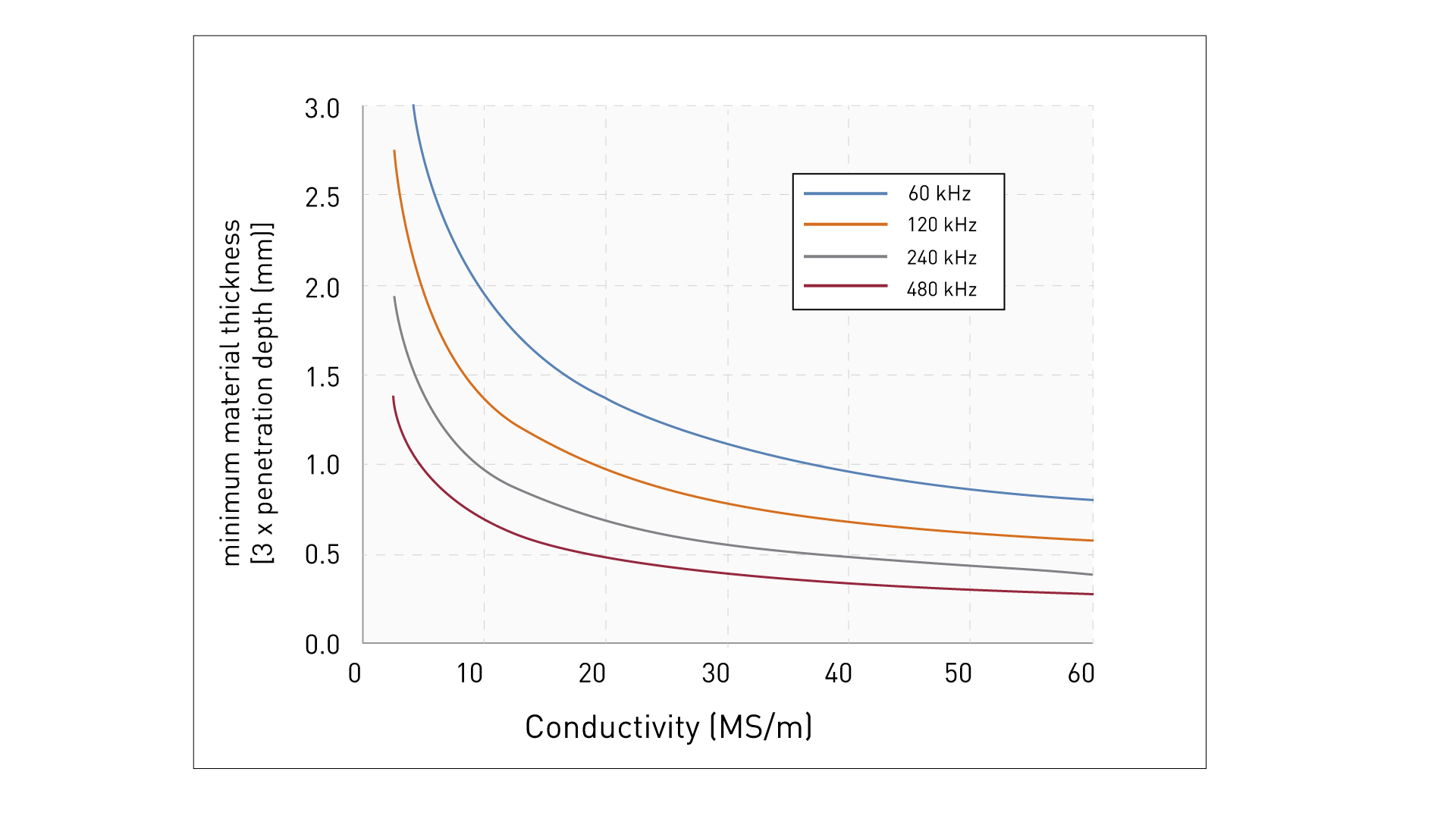
A simple test to determine whether a test object meets the requirements for minimum thickness at the desired measuring frequency can be performed using the copper standard included with the instrument. Here, the standard is placed directly under the test object and it is examined whether the probe measures the conductivity of the test object or of the standard. In the latter case, the test object would be too thin.

4. Curved surfaces

Curved surfaces have a strong influence on the measured value. The smaller the radius of curvature of the measuring object, the more pronounced this influence is. In order to minimize the influence of the curvature on the measurement result, there is on the one hand the possibility to carry out the adjustment ("n-point calibration") on a material with the same curvature. If available, the simpler option is to enter the radius or diameter of curvature directly in the device. The device then corrects the measured conductivity value using the stored relationship between measuring frequency, material and radius of curvature.

Figure 4 shows an example of the percentage deviation of the value of measurement on a special specimen made of copper as a function of the radius of curvature. The deviation is more pronounced for small radii of curvature. A dependence on the measuring frequency is also recognizable.

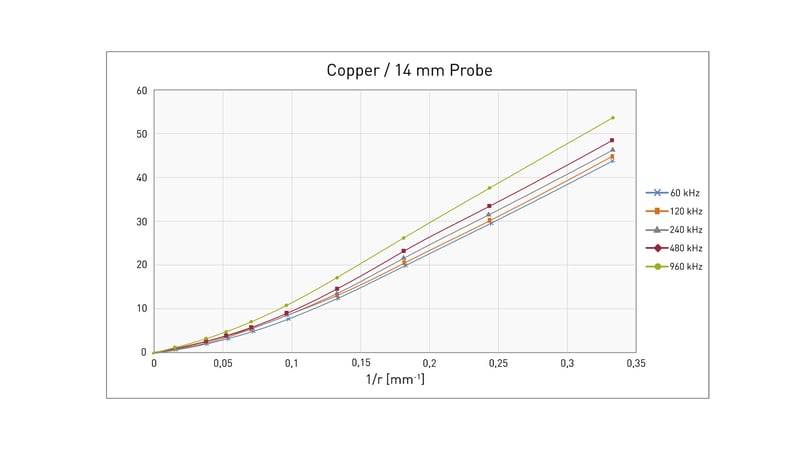
Fig. 4: Percentage deviation of the conductivity measured value as a function of the radius of curvature and the measuring frequency using copper as an example

The influence of curved surfaces can be determined with a correction factor, as shown in the diagrams above.

Another possibility to suppress the influence of curved surfaces in an effective way is to use calibration standards which correspond to the test specimen in their geometric shape. For measurements on curved surfaces, a lowering aid should always be used.

5. Edge effects of conductive measuring probe

The probe of a conductivity meter is electromagnetically shielded at the edges. Figure 5 shows a schematic diagram of the magnetic flux curve for a shielded and an unshielded probe.

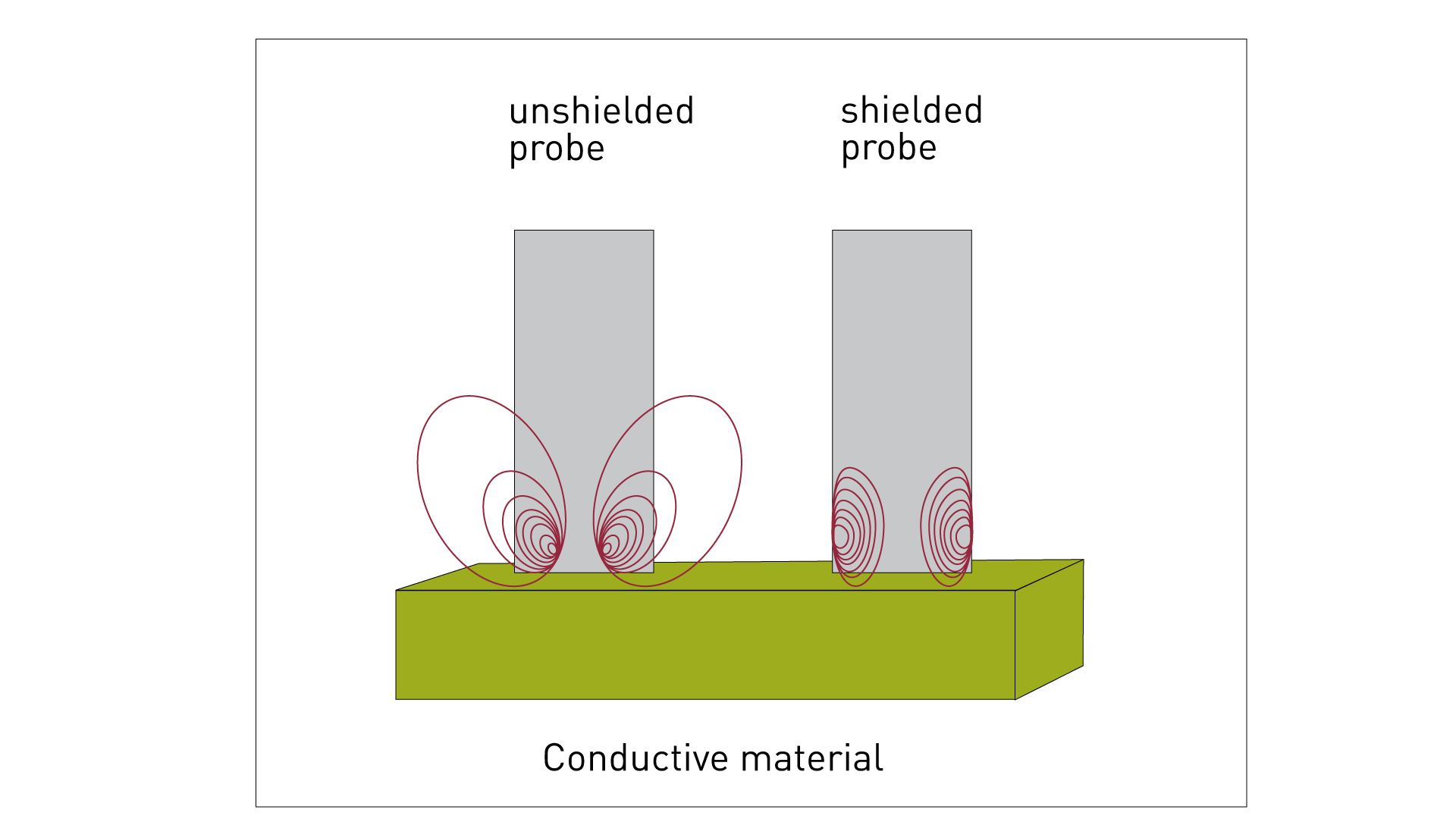
Fig. 5: Magnetic fields in the edge areas of the shielded and unshielded probe

Material or magnetic fields in the edge areas of the shielded probe do not influence the measured value. This means that a measurement with a shielded probe is even possible on the end faces of rods with only 14 mm in diameter. Measurement in bores or milled recesses can also be carried out without error and thus, for example, possible overheating effects on aluminum alloys can be determined.

6. Permeability

A prerequisite for error-free conductivity measurement is that the material under investigation is not magnetizable. Even a low permeability of the material can lead to significant errors in the conductivity measurement.

FOERSTER's product solution for the electrical conductivity measurement

SIGMATEST

FOERSTER has been the market leader for years when it comes to fast, simple and accurate conductivity measuring instruments. With the SIGMATEST, FOERSTER has an established and reliable measuring instrument in its portfolio designed for measuring electrical conductivity. As a case in point, the SIGMATEST is approved for many maintenance applications in aviation. In industry, it is used in the quality control of manufacturing products, the testing of material combinations, and the sorting of metals, alloys, or recyclable materials. The determination of heat damage and in-process inspection in manufacturing and processing in metallurgy are additional fields of application.

Contact our experts and discuss your measuring tasks. We are glad to help you!